BLESS全称:Bloom-filter-based Error Correction Solution for High-throughput Sequencing Reads,即基于布隆过滤器的高通量测序修正方法。
原文链接:https://academic.oup.com/bioinformatics/article-lookup/doi/10.1093/bioinformatics/btu030
1.首先对布隆过滤器的原理进行简单解释。
布隆过滤器[1](Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的。它实际上是由一个很长的二进制向量和一系列随机映射函数组成,布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率(假正例False positives,即Bloom Filter报告某一元素存在于某集合中,但是实际上该元素并不在集合中)和删除困难,但是没有识别错误的情形(即假反例False negatives,如果某个元素确实没有在该集合中,那么Bloom Filter 是不会报告该元素存在于集合中的,所以不会漏报)。相关内容链接:
http://blog.csdn.net/lifuxiangcaohui/article/details/42025629?locationNum=15&fps=1
http://www.dataguru.cn/thread-509369-1-1.html
http://www.cnblogs.com/liyulong1982/p/6013002.html
基本思想
如果想判断一个元素是不是在一个集合里,一般想到的是将所有元素保存起来,然后通过比较确定。链表,树等等数据结构都是这种思路. 但是随着集合中元素的增加,我们需要的存储空间越来越大,检索速度也越来越慢。不过世界上还有一种叫作散列表(又叫哈希表,Hash table)的数据结构。它可以通过一个Hash函数将一个元素映射成一个位阵列(Bit Array)中的一个点。这样一来,我们只要看看这个点是不是 1 就知道可以集合中有没有它了。这就是布隆过滤器的基本思想。
Hash面临的问题就是冲突。假设 Hash 函数是良好的,如果我们的位阵列长度为 m 个点,那么如果我们想将冲突率降低到例如 1%, 这个散列表就只能容纳 m/100 个元素。显然这就不叫空间有效了(Space-efficient)。解决方法也简单,就是使用多个 Hash,如果它们有一个说元素不在集合中,那肯定就不在。如果它们都说在,虽然也有一定可能性它们在说谎,不过直觉上判断这种事情的概率是比较低的。
再结合图像解释一下,布隆过滤器由一个m位的向量BV表示,BV(Bit Vector)初始时是一个全0的向量,采用了p个hash函数映射的方式,输入集合Sin 中含有n个元素,p次hash映射产生p个映射得到的index值,即位置下标值,然后将这些位置的下标置为1
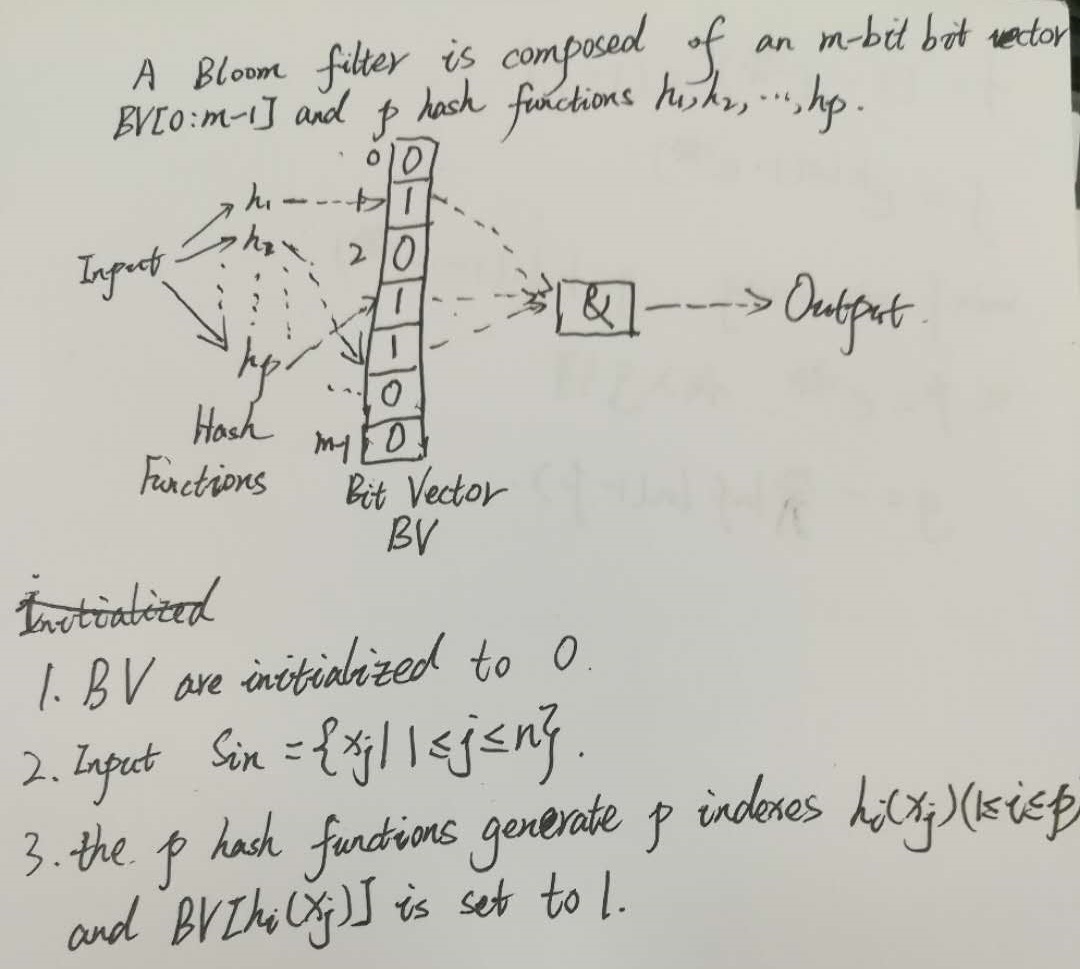
优点
相比于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash 函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储元素本身,在某些对保密要求非常严格的场合有优势。
布隆过滤器可以表示全集,其它任何数据结构都不能;
k 和 m 相同,使用同一组 Hash 函数的两个布隆过滤器的交并差运算可以使用位操作进行。
缺点
但是布隆过滤器的缺点和优点一样明显。误算率(False Positive)是其中之一。随着存入的元素数量增加,误算率随之增加。但是如果元素数量太少,则使用散列表足矣。
另外,一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位列阵变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
赵主任问题:为什么说布隆过滤器存储比其他的数据结构所需内存小?
核心回答内容:布隆过滤器采用的一个n位的向量,可以表示2的n次方个k-mers,所以能节省很多空间。
False positives 概率推导
假设 Hash 函数以等概率条件选择并设置 Bit Array 中的某一位,m 是该位数组的大小,k 是 Hash 函数的个数,那么位数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位的概率是:

那么在所有 k 次 Hash 操作后该位都没有被置 "1" 的概率是:

如果我们插入了 n 个元素,那么某一位仍然为 "0" 的概率是:

因而该位为 "1"的概率是:

现在检测某一元素是否在该集合中。标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 "1",但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中(False Positives),该概率由以下公式确定:

为了让错误率最小,如何确定m,n,k呢?

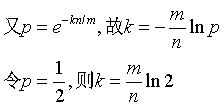
其实上述结果是在假定由每个 Hash 计算出需要设置的位(bit) 的位置是相互独立为前提计算出来的,不难看出,随着 m (位数组大小)的增加,假正例(False Positives)的概率会下降,同时随着插入元素个数 n 的增加,False Positives的概率又会上升,对于给定的m,n,如何选择Hash函数个数 k 由以下公式确定:

此时False Positives的概率为:

而对于给定的False Positives概率 p,如何选择最优的位数组大小 m 呢,

上式表明,位数组的大小最好与插入元素的个数成线性关系,对于给定的 m,n,k,假正例概率最大为:

2.基因纠错相关方法介绍
纠错方法主要可以分为四类:1)k-mer spectrum based,2)suffix tree/array based,3)multiple sequence alignment based,and 4)hidden Markov model based
1)k-mers片段组成集合T,包含基因组中所有的k长度的光谱(连续片段)。如果读入的k-mer不在集合T中,则认为该片段很可能是有错误的。然后用最小的修正代价将该片段改为T中存在的k-mer片段。在没有基因组数据时,我们可以设定一个阈值M,将重复数(计数)大于M的k-mer片段放入集合T,我们将集合中的k-mer片段元素称为可靠的(solid)k-mer段,将不在其中的成为不可靠的(weak)k-mer段。T需要放在内存,这样就能迅速找到weak k-mers的修改方法。T集合的大小随着k的增加会变大。因此,存储T集合的内存使用就受到k的限制。对于一个大数据量的基因组,如果选择的k太小,我们就修改的过程中就会发现,一个weak k-mers可能可以修改成好几个solid k-mers。这样的不确定性,会导致输出的精度问题,因为修改正确性值得怀疑。
2)后缀树和后缀矩阵是处理字符串匹配的主要数据结构。后缀树不是一个存储很高效的数据结构在处理NGS读入时,因为每个基本结构在树中是一个结点的形式出现的。即使很多线性序列处理工具能成功的用后缀矩阵去保存涉及到的序列,维持用后缀矩阵完成NGS读入需要大量的内存空间。所以基于这一结构的纠错方法只能应用与小规模的基因组,即使这样也需要大量的存储空间。HiTEC是最流行的基于后缀矩阵的纠错方法。
?3)基于MSA的方法是用k-mers去创建一个hash表,与读入的k-mer发生关联。对于读入的数据是有着相同的k-mers,序列校准是找到读入中数据中有大量重叠的部分的。这样错误可以得到修正基于共识的序列。但是,基于MSA的方法是不可扩展的,因为读入的数据会导致hash表过大,使得这种方法的计算密集。
4)基于HMM的方法是,读取错误可以通过查找具有最高概率生成读取的状态转换来进行纠正。对于大的基因组很难使用这种方法,因为保存状态和寻找最高概率的转换需要大量的内存使用和较高的计算复杂度。另一种方法使用只有三个状态(插入、删除和匹配)的隐马尔可夫模型对RNA读入错误进行修正。使用MSA对RNA读入数据进行聚类,并为每个簇构建单独的HMM。然而,很难将这种方法应用于大基因组的DNA读取,因为使用MSA进行大量读取的群集读取将非常昂贵。
3.BLESS纠错算法
对于读入长度为L的序列r包含A,C,G,T符号,第i个符号用r[i]表示,0<=i<=L-1. r[i,j]表示r中从第i位到第j位.算法示意图如下:
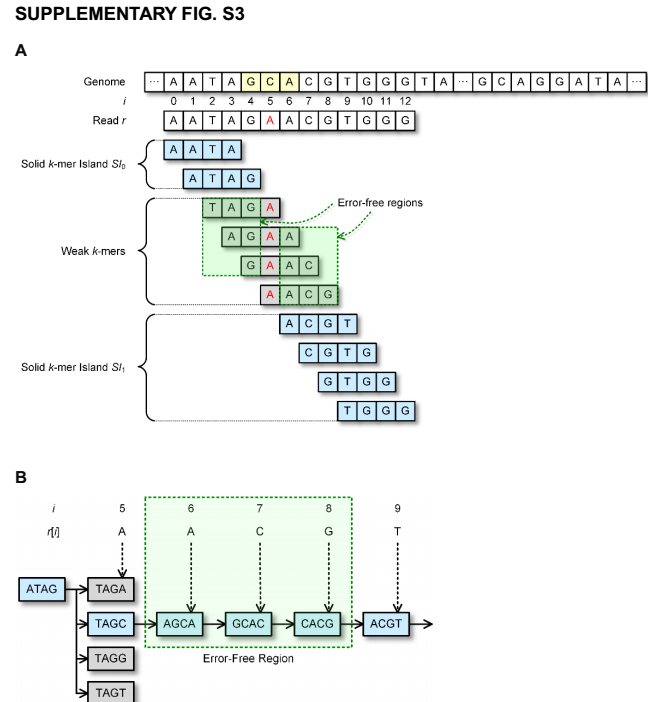
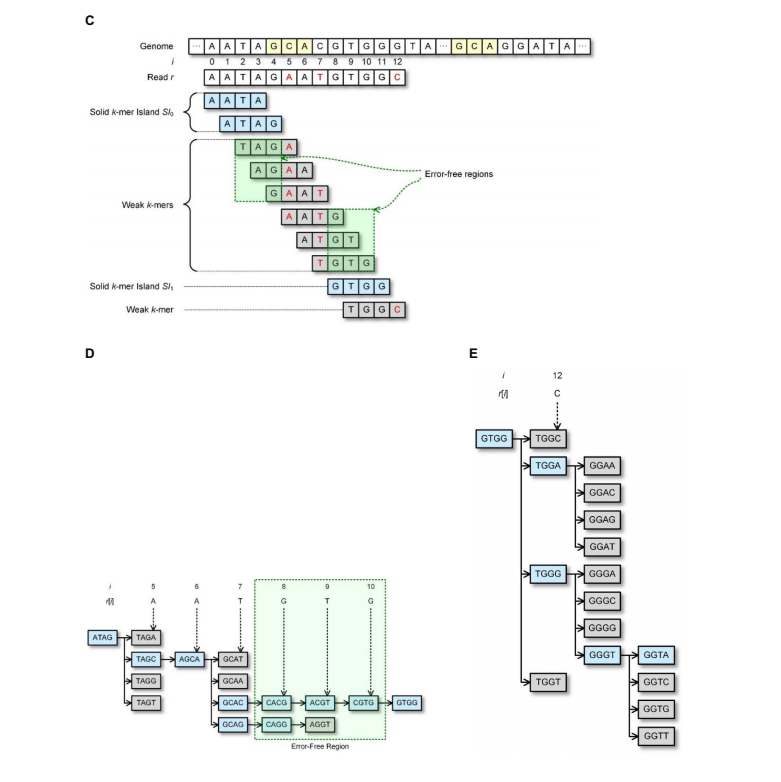
2017.10.16 因研究方向需要,这周转到深度学习与ngs结合相关内容,这部分内容暂时先这样。